완전 탐색

 1. 완전 탐색

  1) 완전 탐색이란?

    - 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법

    - Bruete-force 기법이라고 불린다.

    - 상대적으로 빠른 시간에 문제 해결을 할 수 있다.

    - 일반적으로 경우의 수가 상대적으로 작을 때 유용하다.

    - 우선 완전 탐색으로 접근하여 해답을 도출한 후, 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는 것이 바람직하다.

 

---

 

2. 순열, 조합

  1) 순열(P)

    - 순열이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 있음)

    - nPn은 n!이다.

    - 10!은 약 360만 (마지노선)

 

   2) 조합(C)

    - 조합이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)

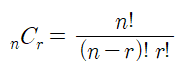
  3)  순열, 조합의 재귀

package com.algo.day2;

import java.util.Arrays;
import java.util.Scanner;

public class 좋은아침 {
	static int N, R;
	static int[] nums, input;
	static boolean[] isSelected;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		R = sc.nextInt();
		isSelected = new boolean[N];
		nums = new int[N]; // 수들을 담을 숫자
		input = new int[R]; // 출력할 숫자 보관

		for (int i = 0; i < N; i++) {
			nums[i] = sc.nextInt();
		}
		
		중복조합(0, 0);
	}

	private static void 중복조합(int cnt, int start) {

		if (cnt == R) {
			System.out.println(Arrays.toString(input));
			return;
		}

		for (int i = start; i < N; i++) {
			input[cnt] = nums[i];
			조합(cnt + 1, i);
		}

	}

	private static void 조합(int cnt, int start) {

		if (cnt == R) {
			System.out.println(Arrays.toString(input));
			return;
		}

		for (int i = start; i < N; i++) {
			input[cnt] = nums[i];
			조합(cnt + 1, i + 1);
		}

	}

	private static void 중복순열(int cnt) {

		if (cnt == R) {
			System.out.println(Arrays.toString(input));
			return;
		}

		for (int i = 0; i < N; i++) {
			input[cnt] = nums[i];
			순열(cnt + 1);
		}
	}

	private static void 순열(int cnt) {

		if (cnt == R) {
			System.out.println(Arrays.toString(input));
			return;
		}

		for (int i = 0; i < N; i++) {
			if (isSelected[i])
				continue;
			input[cnt] = nums[i];
			isSelected[i] = true;
			순열(cnt + 1);
			isSelected[i] = false;
		}
	}
}